
Az új természetszemlélet a jelenlegitől eltérő módon értelmezi a létező valóság jelenségeinek ok-okozati viszonyát, a tényekből, mint sajátos építőelemekből, a jelenlegi egyszerű modell helyett egy új, összetett világot, a Fraktál Univerzumot rakja össze. A Fraktál Univerzum illeszkedik a létező valósághoz és a logika szabályai szerint építkező, ellentmondásmentes gondolati konstrukciónak tűnik. Tekintsünk át a következőkben néhány, a Fraktál Univerzum alapvető működésével és értelmezésével kapcsolatos példát.
1. Tágul-e az Univerzum, léteznek-e gravitációs erők és sötét energiák?
A jelenleg elfogadott, bár sokat vitatott szemlélet szerint az Univerzum tágul, és rendelkezik kezdeti, valamint végállapottal. E szemlélet egyik következménye az úgynevezett ősrobbanás elmélet. Az ősrobbanás elmélet ötlete Gamovtól származik és Slipher, valamint Hubble megfigyelésein alapul. A megfigyelések szerint a galaxisok színképének túlnyomó többsége úgynevezett vöröseltolódást mutat, amely Doppler értelmezése szerint a gyorsulva távolodó mozgás következménye lehet. Ha a részek minden irányban gyorsulva tágulnak, akkor valamikor együtt kellett lenniük, ebből a következtetés láncból nőtte ki magát az elmélet. Ha valami gyorsul, akkor ott Newton dinamikai elképzelései szerint gyorsító erőnek is léteznie kell. A feltételezett gravitációs erők nem gyorsítanak, hanem lassítanak, hiszen vonzó jellegűek, ezért újabb feltételezésekkel kellett élni, amely szerint létezhet sötét anyag és sötét energia is, ők lehetnek azok amik a gyorsítást végzik. Az újabb és újabb feltételezések, egyrészt nem támaszthatók alá ésszerű érvekkel, másrészt nem illeszkednek egy egységes gondolati konstrukcióba, ugyanakkor egyre több újabb megválaszolatlan kérdést vetnek fel.
 Az új természetszemlélet minden
létező jelenséget rendszerminőségként
szemlél, és minden rendszerminőséget az elemi
rendszerek mozgástartalmából származtat. Az
új termszetszemlélet a
létező valóságot egyetlen
fraktál konstrukcióként értelmezi, amelyet
két ellentétes hatású, ugyanakkor
egymást kölcsönösen alakító
fraktál algoritmus hoz létre.
Az új természetszemlélet minden
létező jelenséget rendszerminőségként
szemlél, és minden rendszerminőséget az elemi
rendszerek mozgástartalmából származtat. Az
új termszetszemlélet a
létező valóságot egyetlen
fraktál konstrukcióként értelmezi, amelyet
két ellentétes hatású, ugyanakkor
egymást kölcsönösen alakító
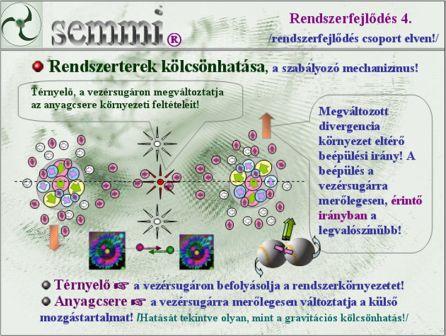
fraktál algoritmus hoz létre. Az elmélet szerint: A létező valóság a primer tér, vagy más fogalomhasználattal élve az elemi homogenitás differenciálódása révén képes megjelenni. Az elemi homogenitástól, vagy az elemi káosztól eltérni, diszkrét módon, kisebb mozgástartalommal, csoportos módon, nagyobb időléptékkel lehet. Ha valamilyen környezetnek nagyobb az időléptéke,akkor az egyben nagyobb élettartamot is jelent. E gondolatmenetből származtatható az egyik univerzális rendszerhipotézis, amely szerint: "Minden rendszer élettartama nagyobb, alrendszerei élettartamánál." E kijelentésnek elképesztő következményei vannak az új természetszemlélet szerinti univerzum modellre vonatkozóan, ugyanis ez csak akkor valósulhat meg, ha a rövidebb élettartamú alrendszerek folyamatosan cserélődnek. Az alrendszerek cserélődése az anyagcsere, amely a sokdimenziós virtuális fraktrál tér minden rendszerszintjén, a rendszerszint időléptékéhez igazodó ritmusban zajlik, azaz: "Minden rendszer anyagcserét folytat". A sokdimenziós virtuális fraktál tér minden rendszerszintje autonóm parciális viselkedést tanúsít, az elemek egyensúlyt tartanak egymással és ebből következően a térforrások és térnyelők konstrukciói között parciális téraramlások alakulnak ki. A bomló rendszerekből távozó alrendszerek egyfajta "térfogati divergenciákként" értelmezhetők, és ők hozzák létre a rendszer állapotkörnyezetét, amely az anygcsere készletét biztosítja. Az új szemlélet logikai építménye szerint a rendszerkörnyezetek is képesek együttműködésre, ha találkoznak. Az ütközve találkozó azonos rendszerszintű rendszerek jó eséllyel bomlanak, a derékszögben találkozó azonos rendszerszintű rendszerek pedig jó eséllyel egyesülnek. A bomló és az egyesülő rendszerek az alacsonyabb és a magasabb rendszerszintek irányában távoznak az azonos parciális viselkedésű környezetből, így mindkét együttműködés térnyelőként jelenik meg. A térnyelők irányában parciális térátrendeződések következnek be, amely a rendszerkörnyezetek anyagcserekészletét módosítja, vagy más kifejezéssel élve megváltoztatja az anyagcsere peremfeltételeit. A változtatás eredményeként a rendszereket összekötő egyenesre merőleges irányú külső mozgáskomponensű csereelemek relatív gyakorisága megnő, ezért az anygcsere során a rendszerek külső mozgástartalmának eredője a rendszereket összekötő egyenesre merőleges irányban módosul. A rendszerek folyamatos együttműködésének következtében, a rendszerek külső mozgástartalmának eredője mindig az összekötő egyenesre merőleges irányban, azaz a pályaérintő irányához igazodik. /Ez azt jelenti hogy a jelenlegi elképzelésekkel ellentétben a valódi mozgatók, nem a rendszereket összekötő egyenes mentén, hanem arra merőleges irányban hatnak, de ez a hatás sem hatás-ellenhatás jellegű, sokkal inkább hasonlítható az elektromágneses jelenségek viszonyához./ A rendszerkörnyezetek ilyen együttműködése, az anyagcsere folyamatos szabályozását és a rendszerek mozgásának összekapcsolódását eredményezi.
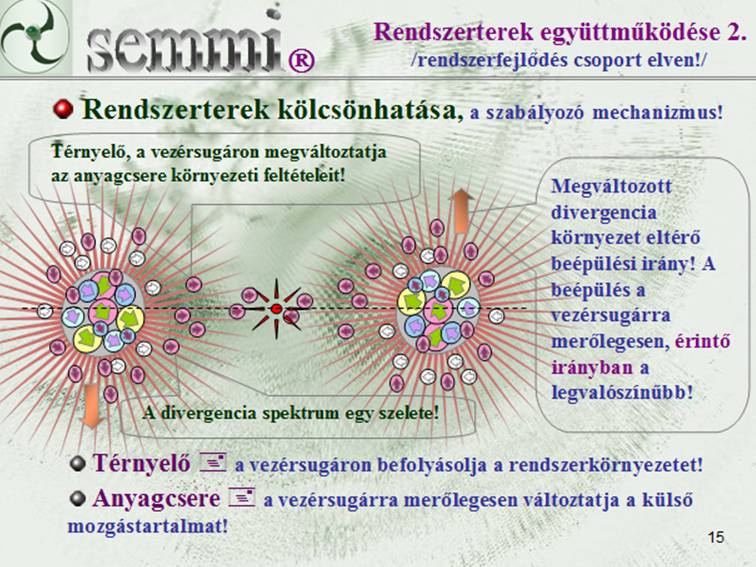 A rendszerek mozgásváltozását a
változó tartalmú anyagcsere idézi elő, az
anygcsere folyamatos változását pedig a
térkörnyezetek együttműködése
következtében fellépő
téráramlások idézik elő.
Érzékelhető, a jelenség, szabályozó
és szabályozott momentumokra tagolódik és
hasonló az elektromos jelenségek körében
ismeretes teljesítményerősítőkhöz. A
jelenség szabályozó eleme jól
közelíthatő Newton
gravitációs erőre
vonatkozó hipotézisével.
A rendszerek mozgásváltozását a
változó tartalmú anyagcsere idézi elő, az
anygcsere folyamatos változását pedig a
térkörnyezetek együttműködése
következtében fellépő
téráramlások idézik elő.
Érzékelhető, a jelenség, szabályozó
és szabályozott momentumokra tagolódik és
hasonló az elektromos jelenségek körében
ismeretes teljesítményerősítőkhöz. A
jelenség szabályozó eleme jól
közelíthatő Newton
gravitációs erőre
vonatkozó hipotézisével. Az új természetszemlélet szerint a feltételezett gravitációs erők nem léteznek. Létezik viszont a folyamatos anyagcsere, léteznek a rendszerkörnyezetek közötti kölcsönhatások, valamint a parciális téráramlások, amelyek képesek szabályozni az anyagcsere feltételeket. Az irányváltoztató rendszermozgásokat a változó anyagcsere, a változó eredő mozgástartalmú anyagcsere elemek idézik elő.
Az előző észrevételekre alapozva a dolgozat úgy véli, hogy az észlelt vöröseltolódási jelenségeket nem a gyorsítő erő irányába mutató gyorsulás, hanem a rendszerminőségek folyamatos szöggyorsulása idézi elő. Az objektumok szöggyorsulása nem idézi elő az Univerzum tágulását, hiszen arra mindig merőleges irányban hat. A dopolgozat elképzelése szerint, az Univerzum folyamatosan, gyorsuló módon, irányváltoztatás jellegűen átrendeződik, de térkörnyezete közel változatlan marad, és nem tágul. Az Univerzum gyorsuló jellegű, ugyanakkor változatlan térkörnyezetű, folyamatos átrendeződése hasonlítható az időjárási jelenségekhez, vagy profán hasonlattal élve, egy szúnyograj esetéhez. A szúnyograjban az egyedek folyamatosan keringve repkednek egy képzeletbeli centrum irányában, de előbb-utóbb mindig a széleken találják magukat, viszont mielőtt kirepülnének a közös térkörnyezetből irányt változtatnak, ezért képesek a rajban maradni. Az egyedek a folymatosan változó irányú mozgással, folyamatosan gyorsuló mozgást valósítanak meg, ennek ellenére, vagy éppen ezért az imbolygó szúnyograj változatlan marad. Ezek után talán érthető a dolgozat elképzelése, amely szerint az univerzum átrendeződése folyamatos gyorsuló mozgásokkal valósul meg, miközben az univerzum nem tágul. Ha az univerzum nem tágul, akkor okafogyott a gyorsítást végző sötét energiák feltételezése, ugyanakkor a sötét anyag léte tényként kezelhető. A sötét anyag nem észlelhető ezért tűnik úgy mintha ő valami különleges misztikus jelenség lenne, de a továbbiakban szereplő értelmezések segítségével tudatunk számára megközelíthetővé válik.
2. Milyen méretű, és milyen viselkedésű az Univerzum?
A jelenlegi hipotézisek szerint az Univerzum viselkedése az őt alakító erők viszonyától függ. Elképzelés szerint az egyik alakító erő a gravitációs erő, amely a tömegtől függ, ezért az Univerzum viselkedése összefügg tőmegével. Ez az elképzelés jelenleg kikezdhetetlennek tűnik, ennek ellenére a dolgozat elveti ezt az elképzelést, mert ez nem illeszkedik az új természetszemlélet logikai építményébe. Az új természetszemlélet szerint a gravitáció elmélete egy a gyakorlatban jól használható modell, de ilyen erőhatások a természetben ténylegesen nem léteznek, nem ők alakítják a létező valóságot.
Az új természetszemlélet szerint: a létező valóság fraktál természetű és egyetlen fraktál konstrukciót alkot. A fraktál konstrukciók egyik alapvető ismérve az önhasonlóság, tehát a fraktál részei hasonlók az egészhez. Más fogalomhasználattal élve a kis univerzum éppen úgy viselkedik mint a nagy. Összegezve, és levonva a következtetéseket: "Az Univerzum viselkedése nem függ méretétől" és tömegjellemzőitől. A dolgozat logikai okfejtése szerint az Univerzum minősége, az ő salyát végtelenhez közeli időléptékében szemlélve állandó. Az Univerzum átrendeződéseit nem gravitációs erők idézik elő, az átrendeződések különös módon erőmentes folyamatokban zajlanak. Az Univerzum átrendeződéseit a kölcsönhatások idézik elő. A kölcsönhatások visszavezethetők az elemi kölcsönhatásokra, amelyek erőmentesek, de a parciális átrendeződési folyamatokban, a rendszerminőségek egyensúlytartási képességéhez kapcsolódóan megjelennek a hatás-ellenhatás jellegű együttműködés formák is. Az egyik rendszeraxióma szerint: "Az új minőség nem hat vissza az alrendszerek minőségére", e szerint a rendszerelemek belső, egymás közötti viszonyában a hatás-ellenhatás kapcsolatok nem érvényesülnek. Az Univerzum nagyléptékű átrendeződési folyamatai a kölcsönhatásokkal állnak közvetlen kapcsolatban, ugyanis ők alkotják a létező valóságot létrehozó algoritmusok elemeit, ezért a newtoni dinamika alaphipotézisei csak mint szabályozó jellegű parciális jelenségek érvényesülnek. A hatás-elenhatás jellegű dinamikai modell elképzelései a parciális téráramlásokhoz, azaz a szabályozás jellegű folyamatokhoz, a rendszerelemek külső kapcsolataihoz illeszthetők. A természet valódi vislkedése erőmentes, e viselkedés részletei a kilencedik részben jelenek meg egy újabb, még összetettebb modell alakjában.
3. Létezik-e sötét anyag, és sötét energia?
A dolgozat elképzelései szerint ilyen minőségek nem léteznek, mert nem illeszkednek a dolgozat logikai építményébe. A dolgozat elképzelése szerint a létező valóság minden minősége rendszerminőség, minden rendszerminőség rendelkezik valamilyen külső mozgástartalommal, és minden külső mozgástartalom rendelkezik irányminőséggel. A rendszerek struktúraelemeiben, egymáshoz viszonyított módon az alrendszerek pozíciótartók, de irányminőségeik minden rendszerszinten körbeforogva egy képeletbeli gömbfelületre mutatnak, ezért eredő értékük zérus közeli. A rendszerek külső irányminősége hatással van az általuk kibocsátott anyagcserespektrum irányminőségére, ez pedig kihat az észlelhetőségre. A dolgozat elképzelése szerint az észlelés tartalma, a jelenségek alrendszerei, rendszerkörnyezetei közötti kölcsönhatások következtében megjelenő új minőségekként azonosítható. Az észlelésnek is értelmezhető irányminősége: Az észlelés iránya, az észlelés folyamatában résztvevő alrendszerek rotáció vektorai által bezárt szöggel azonosítható. Az észlelés tartalma e szög értékével arányos. Ha a jel, és az észlelő receptor rendszereinek külső mozgástartalom vektorait {v1} és {v2}, jelőli, továbbá az általuk bezárt szög értéke {g}, akkor az észlelés tartalma:
{Et ~> |v1 |* | v2 |* sin(g)}. Az összefüggés szerint ha a jel és a receptor külső mozgásminőség vektorai közel párhuzamosak, akkor a jelenség nem észlelhető, hiszen {sin(g) = 0} /Részletek a második dolgozatrészben találhatók!/
Az előző okfejtésre alapozva, a dolgozat úgy véli, sötét anyag és sötét energia nem létezik, de létezik bizonyos pozíciókból nem észlelhető anyag. Mi sem vagyunk és
 zlelhetők
bizonyos
térpozíciókból. Más
aspektusból szemlélve, a természet fraktál
elemei között minden rendszerszinten léteznek
hasonló irányminőséggel rendelkezők, ők nem
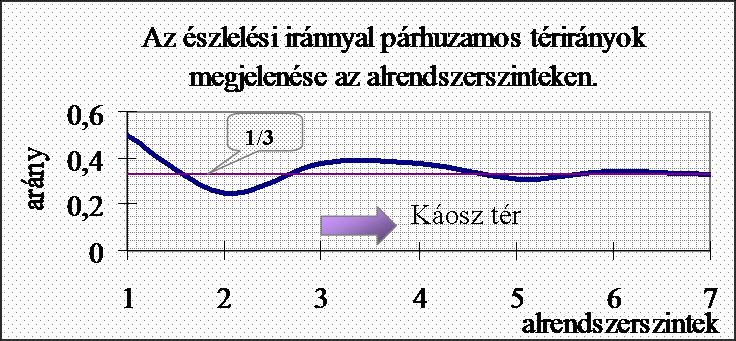
észlelhetők egymás számára. Az egymás számára nem észlelhető
minőséghalmaz aránya rendszerszintenként változik, de az {1/3}arányhoz
tart. A dolgozat elképzelése szerint az észlelő számára a legkedvezőbb észlelési irány esetén,
sem jelenik meg a mozgási állapot szempontjából észlelhető jelenségek köréből,
a magasabb rendszerszintek egyharmada, az alacsonyabb rendszerszintek 50-75%.
A dolgozat elképzelése szerint a nem
észlelhető anyag, itt van az orrunk előtt, vele együtt
egymásban létezünk, a mi alkotórészeink egy része is ilyen. A nem
észlelhető anyagtól mindössze csak a külső
mozgástartalom irányminőségében
különbözünk. A megértést
segítő, de nem autentikus, viszont szemléletes
példával élve, az észlelhető és nem
észlelhető anyag hasonlóan viselkedik, mint a lemezes
sötétítő szerkezet. Ha a lemezek síkja
merőleges az ablakra, akkor átlátunk rajta és
megjelenik a külső környezet, ha viszont a lemezek
síkja párhuzamos az ablak síkjával, akkor
nem látunk ki, akkor a lemezeket látjuk.
zlelhetők
bizonyos
térpozíciókból. Más
aspektusból szemlélve, a természet fraktál
elemei között minden rendszerszinten léteznek
hasonló irányminőséggel rendelkezők, ők nem
észlelhetők egymás számára. Az egymás számára nem észlelhető
minőséghalmaz aránya rendszerszintenként változik, de az {1/3}arányhoz
tart. A dolgozat elképzelése szerint az észlelő számára a legkedvezőbb észlelési irány esetén,
sem jelenik meg a mozgási állapot szempontjából észlelhető jelenségek köréből,
a magasabb rendszerszintek egyharmada, az alacsonyabb rendszerszintek 50-75%.
A dolgozat elképzelése szerint a nem
észlelhető anyag, itt van az orrunk előtt, vele együtt
egymásban létezünk, a mi alkotórészeink egy része is ilyen. A nem
észlelhető anyagtól mindössze csak a külső
mozgástartalom irányminőségében
különbözünk. A megértést
segítő, de nem autentikus, viszont szemléletes
példával élve, az észlelhető és nem
észlelhető anyag hasonlóan viselkedik, mint a lemezes
sötétítő szerkezet. Ha a lemezek síkja
merőleges az ablakra, akkor átlátunk rajta és
megjelenik a külső környezet, ha viszont a lemezek
síkja párhuzamos az ablak síkjával, akkor
nem látunk ki, akkor a lemezeket látjuk. 4. Mi történik a fekete lyukakban és az égítestek középponti részein?
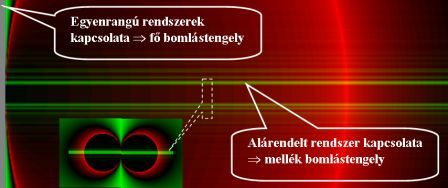
E kérdésekre az elmélet általános, minden rendszerre érvényes választ képes megfogalmazni egy rendszerhipotézis formájában. A hipotézis megfogalmazása előtt szemléljük ismét, az előzőkben szereplő példát, két egyenrangú rendszer környezetének együttműködését. Egyenrangú rendszerek, környezete is egyenrangú, így hasonló, ezért a találkozás jellege szimmetrikus. Belátható, a kialakuló térnyelők pozíciója, relatív dúsul a rendszerek közötti szimmetriasík környékén. Az együttműködő rendszerkörnyezetek lehetnek nem egyenrangúak is, mi történik ezekben az esetekben? Belátható, ezekben az esetekben a térnyelők relatív feldúsulása nem a felező szimmetriasík környezetében helyezkedik el, hanem eltolódnak a kisebb anyagcsere spektrumot kibocsátó rendszer irányában. Létezhet a jelenség eseményhalmazának szélsőértéke? Igen létezhet, mégpedig az abszolút domináns-, és az abszolút alárendelt rendszerkapcsolatok esetében. Ilyen rendszeregyüttműködésekben a térnyelők pozíciója a rendszereket összekötő egyenes mentén eltolódik az alárendelt rendszer irányában és szélsőértékben megeggyezik az alárendelt rendszer centrum részével. E kijelentések tartalmi lényege megfogalmazható a következő alakban is: "A domináns rendszer maga körül, keringő pályára kényszeríti az alárendelt rendszert, miközben bontja és elvonja annak struktúra és állapotkörnyezetét."
Mivel minden rendszer része a természet fraktál konstrukciónak, ezért "minden rendszer egyidejűleg domináns és alárendelt szerepben létezik." Domináns szerepben elvonja az alárendelt rendszerek anyagcserekészletét, alárendelt szerepben viszont átadja saját anyagcserekészletét az ő domináns rendszerének, ezért léte a dinamikus egyensúlytól függ. E kijelentés tartalmi lényege ismét megfogalmazható minden rendszerre érvényes hipotézisként: "Minden rendszer belülről fogyatkozik, kívülről pedig gyarapszik."

Mi történik például a föld nevű bolygó esetében?
Kívülről záporoznak rá a különféle meteoritok, ritkán a kisbolygók, a napszélből származó úgynevezett korpuszkuláris sugárzás és a különféle elektromágneses sugárzások, ezek jelentős részét a föld befogja és ezáltal kívülről gyarapszik. Ez szinte kézzelfogható, de mi van a centrum részen, mi termeli a hőt és miért van a vulkáni tevékenység, továbbá, miért vándorolnak a kéreglemezek?
 Az előző
okfejtés szerint ezek a jelenségek is
érthetővé válnak,
hiszen a domináns rendszer, a föld esetében a nap,
saját sugárzásával bomláscentrumot
működtet a föld középpontjában
és a bontott anyagot elvonja. A bontott és elvont
anyagcserekészlet spektrumot alkot, és
valószínűsíthetően a fotonok rendszerszintje
alatti tartományokat képvisel, ezért
jórészt akadálytalanul
átjárják a magasabb rendszerszintű
struktúraelemeket, de azért a rendszerszintek
között is valamilyen valószínűséggel
léteznek parciális egyensúlytartó jellegű
kapcsolatok, ezért a rendszerszintek viszonyában egyfajta
hatásláncolat-szerű hatáshullám jelenik
meg. Mivel a bontott rendszerek
mozgástartalma hatványfüggvény szerint nő,
ezért a hagyomásnyos értelemben vett,
mozgási energiának nevezett jellemző is hasonlóan
viselkedik, és a rendszerszintek
hatáslácolatán keresztül a magasabb
rendszerszinteken, például az atomok
rendszerszintjén, egyszercsak
hőenergiaként jelenik meg. Mivel a vas atom a legstabilabb az
atomi rendszerszinten, ezér bomlik ő a többi atom
után. Ezért található vas a bolygók
centrum részén, nem pedig a gravitáció
hatása miatt. Érzékelhető a belső
fogyatkozás is, ugyanis a föld anyaga lassan, de
folyamatosan áramlik a centrum felé, ahonnan a nap
által működtetett bontócentrumon, vagy más
fogalomhasználattal élve térnyelőn keresztül
távozik. Más aspektusból szemlélve a
föld folyamatosan zsugorodik, belülről fogyatkozik,
felszíne csökken, ez okozza a kéreglemezek
egymásra torlódó mozgását és
a vulkáni tevékenységet. Különös
módon nem a feltörő láva okozza a
kéreglemezek mozgását, hanem a kéreglemezek
centrum irányú mozgása idézi elő a
láva feltörését, amely aztán visszahat
a kéreglemezek felületi mozgására. A
kéreglemezek
centrum irányú, valamint a gömfelületen
történő mozgásai,
szabályozó-szabályozott,
Az előző
okfejtés szerint ezek a jelenségek is
érthetővé válnak,
hiszen a domináns rendszer, a föld esetében a nap,
saját sugárzásával bomláscentrumot
működtet a föld középpontjában
és a bontott anyagot elvonja. A bontott és elvont
anyagcserekészlet spektrumot alkot, és
valószínűsíthetően a fotonok rendszerszintje
alatti tartományokat képvisel, ezért
jórészt akadálytalanul
átjárják a magasabb rendszerszintű
struktúraelemeket, de azért a rendszerszintek
között is valamilyen valószínűséggel
léteznek parciális egyensúlytartó jellegű
kapcsolatok, ezért a rendszerszintek viszonyában egyfajta
hatásláncolat-szerű hatáshullám jelenik
meg. Mivel a bontott rendszerek
mozgástartalma hatványfüggvény szerint nő,
ezért a hagyomásnyos értelemben vett,
mozgási energiának nevezett jellemző is hasonlóan
viselkedik, és a rendszerszintek
hatáslácolatán keresztül a magasabb
rendszerszinteken, például az atomok
rendszerszintjén, egyszercsak
hőenergiaként jelenik meg. Mivel a vas atom a legstabilabb az
atomi rendszerszinten, ezér bomlik ő a többi atom
után. Ezért található vas a bolygók
centrum részén, nem pedig a gravitáció
hatása miatt. Érzékelhető a belső
fogyatkozás is, ugyanis a föld anyaga lassan, de
folyamatosan áramlik a centrum felé, ahonnan a nap
által működtetett bontócentrumon, vagy más
fogalomhasználattal élve térnyelőn keresztül
távozik. Más aspektusból szemlélve a
föld folyamatosan zsugorodik, belülről fogyatkozik,
felszíne csökken, ez okozza a kéreglemezek
egymásra torlódó mozgását és
a vulkáni tevékenységet. Különös
módon nem a feltörő láva okozza a
kéreglemezek mozgását, hanem a kéreglemezek
centrum irányú mozgása idézi elő a
láva feltörését, amely aztán visszahat
a kéreglemezek felületi mozgására. A
kéreglemezek
centrum irányú, valamint a gömfelületen
történő mozgásai,
szabályozó-szabályozott, 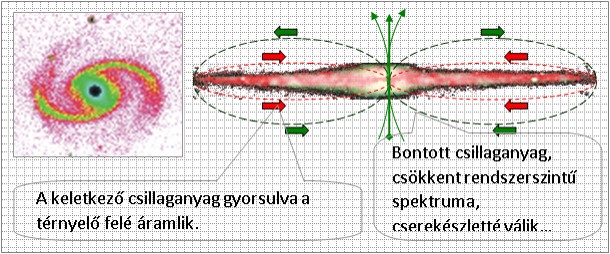 vagyis vektorszorzat
jellegű viszonban léteznek.
vagyis vektorszorzat
jellegű viszonban léteznek.Az elmélet szerint a bontócentrum minden rendszer centrum részén megtalálható, hiszen minden rendszernek létezik domináns rendszere, amelyik ezt létrehozza és fenntartja. Ilyen bontócentrum található különösen látványos formában a galaxisok centrum részén is. A fekete lyukak nem egyebek mint bontócentrumok, ahol a spirálkarokon forogva, gyorsuló ütemben közelítő csillagrendszerek és bolygók bontásra kerülnek, bontás után pedig szétsugárzódnak. A szétsugárzott csaillaganyag más galaxisokból származó anyagcserespektrumokkal további ismétlődő együttműködésekben vesz rész, és bizonyos peremfeltételek teljesülése esetén újabb galaxisok keletkeznek. Ilyen módon képes a "Nagy Egész" folyamatosan átrendeződni.
 A rendszerekben működő bontócentrumok
fraktál konstrukcióba rendezhetők.
Valószínűsíthetően e konstrukciók egyik
szélsőértékeként
azonosíthatók a fekete lyukak. A csillagok és a
bolygók a galaxisok forgó spirálkarjain
keletkeznek és létük a bontócentrum
megközelítésével véget ér, de a
galaxisok, mint különös konstrukciók
működnek tovább saját időléptékük
szerint. Az új szemlélet szerint csak a "Nagy
Egész" időtlen jelenség, ezért a galaxisoknak is
van élettartamuk. A galaxisok élettartama
valószínűsíthetően a dinamikus egyensúly
megbomlásával ér véget, ekkor
szétsugározzák saját
anyagcserekészletüket és tartalmi
lényegük a továbbiakban nem képes
megnyilvánulni.
A rendszerekben működő bontócentrumok
fraktál konstrukcióba rendezhetők.
Valószínűsíthetően e konstrukciók egyik
szélsőértékeként
azonosíthatók a fekete lyukak. A csillagok és a
bolygók a galaxisok forgó spirálkarjain
keletkeznek és létük a bontócentrum
megközelítésével véget ér, de a
galaxisok, mint különös konstrukciók
működnek tovább saját időléptékük
szerint. Az új szemlélet szerint csak a "Nagy
Egész" időtlen jelenség, ezért a galaxisoknak is
van élettartamuk. A galaxisok élettartama
valószínűsíthetően a dinamikus egyensúly
megbomlásával ér véget, ekkor
szétsugározzák saját
anyagcserekészletüket és tartalmi
lényegük a továbbiakban nem képes
megnyilvánulni. 5. Rövidülnek-e a mérőrudak, lassulnak-e az órák, létezik-e széle és közepe az univerzumnak?
E kérdések megválaszolása, a jelenlegi szemléletre és néhány kísérleti eredményre alapozott módon, a misztika világába repíti a közönséges halandók sokat próbált tudatát. Az új természetszemlélet szerint e kérdésekre ellentmondás-, és misztikamentes válaszok adhatók, bár e válaszok elfogadása és megértése sem egyszerű feladat.
Az új természetszemlélet szerint a mérőrudak nem rövidülnek, az órák pedig nem váltanak ritmust, nem a térméret és nem a ritmus az ami változik, az esemény és az észlelő közötti viszony, valamint az észlelhetőség az ami változik. Az új természetszemlélet szerint a foton nevű részecskék külső mozgástartalma nem képez felső szélsőértéket, az ő rendszerminőségét generáló alrendszerek és az alrendszerek alrendszerei hatványfüggvény szerint növekvő külső mozgástartalommal rendelkeznek. E részek és a részek-részeinek külső mozgástartalma nem állandó, hiszen ők is folytatnak anyagcserét, amely a külső anyagcsere környezettől függő módon változik, így a rendszerminőség külső és belső mozgástartalma is változik. A megértést segítve tekintsünk át egy a dolgozat tizedik részéből kiemelt részletet:
Az új természetszemlélet, rendszerekben, rendszerminőségekben, szélsőértékekben és átmenetekben, meg határátmenetekben gondolkozik, ennek következtében jelenik meg a létező valóság fraktál természete. E módon lehetséges a létező valóság jelenségeinek egyetlen minőségparaméterből, az elemi mozgástartalomból való ellentmondásmentes származtatása. Elképzelhető más gondolati konstrukció is, amely alkalmas a létező valóság megközelítésére, de az új természetszemlélet már létezik, egyfajta szerszámkészletként alkalmazható, ellentmondásmentesnek tűnik és a tapasztalatok szerint, illeszkedik a létező valóság jelenségeihez. Ember, hát ezek szerint az „a-priori” elemi mozgástartalmakként elfogadott jelenségek nem is léteznek? Abszolút értelemben nem! Az emberi elme nem képes érdemi információt szerezni a létező valóság tényleges természetéről. Az emberi elme csak a nem ismert minőségek viszonyával kapcsolatban képes elképzeléseket kialakítani, kijelenthető az emberi elme csak a relatív valóságot képes megközelíteni az abszolút létezőt viszont nem. A rendszerminőségek nem abszolút létezők ők ugyanis a struktúrák és állapotok viszonyából fakadnak, a szélsőértékekként feltételezett minőségek, a „Nagy Egész” és az „elemi részek” minőségei nem ilyenek ők határátmenetekként jelennek meg ők nem rendszerminőségek. /A megértés szempontjából, tudatunk számára célszerű lehet, ha a rendszerminőségek vetületi aspektusát hangsúlyozzuk. E szerint minden rendszerminőség vetületi minőségben észlelhető, vagy más aspektusból szemlélve a különböző dimenziótartományokban csak vetületeik által léteznek. Az elemi rendszerek, mint szélsőértékek, szemlélhetők olyan rendszerminőségekként, amelyeknek a szemlélő térszektorába eső vetületi minősége zérus közeli, ez azt jelenti, nem észlelhető irányminőségű, vagy nem ebben a dimenziószektorban létező rendszerminőségekről van szó, ezért lehet a térkörnyezete zérus közeli ugyanakkor a mozgástartalma végtelen közeli. Profán példa lehet a fűszálakon szaladgáló bogarak oldal-, és felülnézeti jelensége./
Ember, hát milyen elmélet az, amely nem létező tényeken alapul? Az új természetszemlélet létező tényeken alapul, de a létezés minősége nem abszolút, hanem csak relatív. Nem zagyvaság ilyeneket állítani? Nem, de a további magyarázkodás helyett a megértés érdekében végezzünk el egy gondolatkísérletet és vizsgáljuk meg az alma nevű gyümölcs különös jelenségét. /A hagyományok szerint az alma az eredetmondák és a gravitáció elméletében is alapvető jelentőségű./Válasz: az almának a gyümölcsfejlődés során nem növekedik bal, vagy jobboldala ő egyszerűen csak alma, ezért abszolút értelemben az almának nem létezik bal meg jobb oldala, így abszolút értelemben a jobb és baloldala közötti átmeneti jelenségek sem léteznek. Ezek a minőségek az alma és a szemlélő relatív viszonyában jelennek meg.
Kérdés: Relatív értelemben hány darab bal meg jobboldala lehet az almának?
Válasz: Relatív értelemben az almának annyi bal meg jobboldala létezik, ahány szemlélője akad, azaz a jobb és a baloldal csak az alma és a szemlélő viszonyában megjelenő rendszerminőség. E viszonyban a szemlélők képesek a bal és a jobboldali minőségek közötti átmeneti minőségeket is felismerni. /Ember hát az alma mindenhol alma nem átmeneti jelenség! Az íz szempontjából igen, de az észlelhető vetületi minőségek szempontjából nem./
Tegyük fel a kérdést létezhet-e az univerzumnak közepe, széle, alsó vagy felső része? A polgárpukkasztó jellegű kérdésre egyértelmű válasz adható, nem, nem létezhet. Az Univerzum szélsőérték, vele kapcsolatban az emberi elme által kreált fogalmak tartalma nem alkalmazható, ugyanis ezek a minőségek a jelenség és a szemlélő viszonyában megjelenő új minőségek, mivel azonban a „Nagy Egész” minden létező jelenséget magában foglal, ezért rajta kívül nem létezhet semmi, tehát nem létezhet szemlélő sem így olyan viszony sem, amelyben e minőségek megjelenhetnének.
A létező valóság elképesztő, szinte misztikus természete jelent meg előttünk. Az alma minden szemlélő számára eltérő vetületi minőségben jelenik meg. Ez az új minőség a szemlélő pozíciójától, relatív rendszerszintjétől és a szemlélés időléptékétől függ. Mit jelent az alma vetületi minősége? Nos, az alma ténylegesen az egymásba csomagolt alrendszereinek mozgása által kifeszített sokdimenziós virtuális térben létező jelenség, de a háromdimenziós valós térben jelenik meg, ezért számunkra háromdimenziós jelenségnek tűnik, viszont a szemlélő számára csak a felülete észlelhető, annak is csak a kétdimenziós vetületei, de az sem mindenhol. Hát egy almának nem csak egyetlen vetületét látjuk? Nem bizony, egy nézetben, sokféle vetületet látunk. Amíg az alma középrészére teljes rálátással bírunk, addig a szélek csak közel zérus kiterjedésű élekben látszanak. Mi történt?
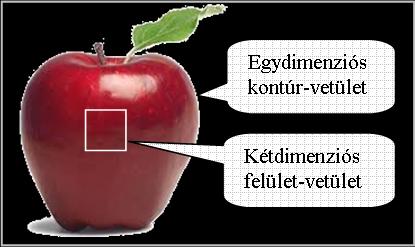 Az történt,
hogy az alma fraktál minőségben jelent meg számunkra, ugyanis a bal és jobb
széleken a kétdimenziós felület, csak egydimenziós határvonalként,
szélsőértékként látható, a szélek között pedig a felületelemek vetületei
fokozatos átmenetekben más-más vetületi minőségekben jelennek meg. A fraktál
szinteken elhelyezkedő minőségek is hasonlók, ők a szélsőértékek lineáris
kombinációi, fokozatosan fordulnak ki a magasabb dimenziótartományt képviselő
virtuális tér irányában, ezért képviselnek tört dimenzióértékeket.
Az történt,
hogy az alma fraktál minőségben jelent meg számunkra, ugyanis a bal és jobb
széleken a kétdimenziós felület, csak egydimenziós határvonalként,
szélsőértékként látható, a szélek között pedig a felületelemek vetületei
fokozatos átmenetekben más-más vetületi minőségekben jelennek meg. A fraktál
szinteken elhelyezkedő minőségek is hasonlók, ők a szélsőértékek lineáris
kombinációi, fokozatosan fordulnak ki a magasabb dimenziótartományt képviselő
virtuális tér irányában, ezért képviselnek tört dimenzióértékeket. Nagyon különös, eddig nem gondoltunk arra, hogy az alma számunkra észlelhető egyetlen nézete több, eltérő dimenziótartalmú, szeletkét tartalmaz, de ez a fraktál természet egyik sajátossága, ilyen a létező valóság valódi arca. Valószínűsíthetően a hindu vallásfilozófia hasonló megfontolásból alakított ki olyan elképzelést, amely szerint Visnu istenség végtelen számú minőségaspektussal rendelkezik.
Összegezve az előző gondolatmenetet, hipotézisként rögzíthető:
A rendszerminőségek, egymás közötti viszonyukban, vetületben jelennek meg. A minden létezőt magába foglaló „Nagy Egész” nem kerülhet külső szemlélővel viszonyba, ezért nem rendelkezik külső vetületi minőségekkel.
A „Nagy Egésznek” nincs közepe, vagy széle, az alma bal-, vagy jobboldala nem fogyasztható!
Ember a kukac pontosan tudja hol az alma közepe és a széle,
pedig nem külső szemlélő! Igen de a magzóna állománya különbözik az alma többi
állományától, az alma esetében a minőségkülönbség eligazít, létezik
viszonyítási lehetőség, a „Nagy Egész” sajátléptékében viszont átlagosan
mindenhol azonos homogenitással rendelkezik, ezért nem létezik viszonyítási
lehetőség.
A létező valóság fraktál természete lenyűgöző, de tartalmi lényege nem
közelíthető meg egyszerű olvasás útján kreatív együttgondolkozás és saját
elképzelések kifejlesztése nélkül.
A dolgozat logikai építménye szerint e jelenségek objektív módon nem létezhetnek. Ha nem létezhetnek, akkor mégis mivel magyarázható megjelenésük a tudományos gondolkozás területén? A dolgozat elképzelése szerint a kísérleti eredmények észlelésével és az extrapolációkon alapuló értelmezésekkel kapcsolatos a jelenség. E jelenség csoport sem megelepőbb, az ősrobbanás elmélet, a mérőrudak rövidülése, vagy a gravitációs távolhatás elképzeléseinél.
¤ Léptékek és dimenziók: A dolgozat elképzelése szerint e furcsaságok egy része a dimenzióváltás jelenségével és a sajátléptékek kérdésével függhetnek össze. Vegyünk egy gyakorlati példát konkrétan a rezgő húr esetét. A nyugalomban lévő húr, jó közelítéssel egydimenziós jelenség és konkrétan ott tarózkodik ahova kifeszítik. A rezgő húr időben változó helyeken esetlegesen van jelen, a kritikus állapotban rezgő húr úgy viselkedik mintha kétdimenziós jelenség lenne. A dimenzióváltás jelensége rendszerszint váltást jelent. A rendszerminőségek saját időléptékben szemlélve képesek megjelenni, hiszen ők egymásba csomagolt forgó szerkezetek, amelyek virtuális terét az alrendszerek mozgása feszíti ki. Ha az alrendszerek időléptékében szemléljük őket akkor az alrendszerek jelennek meg. A rezgő húr esetében is hasonló a helyzet. Ha felvételt készítünk a jelenségről az ő saját időléptéke szerint, akkor a húr elmosódott képe megjelenik a sajátrezgések által lefedett területen és úgy tűnik mindenhol ott van egyidejűleg, de ha a saját időléptéknél kisebb expozíciós idejű felvételeket készítünk, akkor nyilvánvalóvá válik, hogy a húr a terület biozonyos részén csak időben egymást követő módon, egymást követő fázisálapotokban van jelen. Ha az észlelés tartalma szerint egy részecske egyidejűleg két helyen tartózkodik, akkor ez az egyidejűség az új rendszerminőség sajátléptéke szerint értendő.
Az időkésleltetés nélküli hatásterjedés, a távolhatás is varázslatos jelenség, de a dolgozat elképzelése szerint a rendszerszminőségek mozgásállapota csak és kizárólag az anyagcserével kapcsolatban, az anyagcsere következtében változhat, az anyagcsere, pedig az alrendszerek kibocsátásával és befogadásával kapcsolatos jelenség, amely téráramlásokat feltételez. A téráramlások az őket alkotó rendszerek külső mozgástartalmához igazodó parciális jelenségek. A dolgozat elképzelése szerint nem léteznek időkésleltetés nélküli
távolhatások.
Úgy tűnik a körülöttünk létező valóság annyiféle arcát mutatja felénk, ahányféleképpen szemléljük. A jelenségek folytonosnak tűnnek, vagy diszkrétnek, a szemlélés időléptékétől függően, esetenként nem dönthető el, hogy az észlelés tartalmát sok ténylegesen jelenlévő, vagy néhány relatív gyorsan mozgó és csak esetlegesen jelenlévő minőség generálja. A dolgozat elképzelése szerint: "Az Univerzum, az esemény és a szemlélő viszonyítási rendszerének relatív különbségétől függő minőségben, a szemlélés időléptékétől függő rendszerszinten jelenik meg, egyedi, vagy összesített kép formában.”
¤ Időutazás és a féreglyukak: Bizonyára többen vannak olyanok akiket a bulvár sajtó elkerül, de érdeklődéssel olvassák a különféle tudományos elképzeléseket a lehetséges időutazásokról, térugrásokról és más hasonló csodálatba ejtő jelenségekről. E jelenségek a "téridő" /ez egy kitalált fogalom/ különleges pontjaihoz az úgynevezett féregjáratokhoz, egymástól távoli térkörnyezeteket összekapcsoló egyfajta különös kürtőkhöz kötődnek. Az elképzelések szerint ilyen különleges helyek lehetnek a fekete lyukak, ha tehát más téridőben, például egy távoli galaxis valamelyik kellemes űrvendéglőjének teraszán szeretnénk elfogyasztani az ebéd utáni kávénkat, akkor ezt egy ilyen időalagúton történő áthaladással kellene megoldani. Az elme különös víziókat képes megjeleníteni, de ezek a víziók illeszkednek-e a létező valósághoz? Milyen válaszok adhatók e felvetésekre az új természetszemlélet segítségével?
¤¤ Az idő-, és a téralagutak természete: A tudomány és ezen belül a csillagászat egyik megdöbbentő felfedezése volt a galaxisok központi részén található fekete lyukak léte. Valóban különös jelenségek, de csak ott vannak és csak olyan különc minőségben léteznek? A megfigyelt és a gravitáció elméletével értelmezett fekete lyukak többen vannak, eltérő méretűek és még képesek egymással egyesülni is.
Az új természetszemléletnek nevezett elképzelés szerint, ami létezik, az mind fraktál természetű, és egyetlen természet fraktál alakzatba rendezett módon létezik, következésképpen a fekete lyukak is fraktál természetűek és a természet fraktál rész alakzatként létezik önálló fraktál alakzatuk. E fraktál alakzat illeszkedik a rendszerminőségek fraktál alakzatához. A dolgozat elképzelése szerint a fekete lyukak a galaxis rendszerszinthez kapcsolható úgynevezett "bontó centrumok". Bontó centrum működik minden rendszer centrum részén, az egyik alapvető rendszerhipotézis szerint: "Minden rendszer kívülről gyarapodik, belülről fogyatkozik". Ez a jelenség, a gyarapodás és a fogyatkozás, a rendszerek anyagcsere folyamataival azonosítható. Vegyük az élőlények példáját, ők is rendszerek, ők is folytatnak anyagcserét, mint ahogy minden más rendszer is. Az élőlények anyagcserélye a külső környezetből felvett különböző szintű rendszerek befogadásával kezdődik. A felvett anyagcsere elemek a szervezeten belüli bontócentrumokba kerülnek, ahol alkotóelemekre, azaz alrendszerekre bomlanak és ebben az állapotban képesek a szervezetbe beépülni. Belátható a sárgarépa elveszti rendszerminőségét mielőtt a nyuszi szervezetébe beépülne. Az anygcsere további részében a bontócentrumon keresztűl a szervezet kibocsátja a korábban felvett anyagok egy részét, de ez a kibocsátás alacsonyabb rendszerszinteken történik. A rendszerek, ezen belül a különféle élő szervezetek fraktál természetűek, alrendszerekből és az alrendszerek további alrendszerekből építkeznek, ezért az anyagcsere minden rendszerszinten minden rendszer esetében, különböző időléptékek szerint folyamatosan zajlik, ezért úgy az anyagcsere elemek befogadása, mint azok kibocsátása spektrum jellegű, különféle rendszerszintű elemek halmaza.
A bontó centrumok különféle, de osztály szinten hasonló minőségekben léteznek minden rendszer centrum részén. E bontó centrumok térméretük időléptékük és a befogadott valamint a kibocsátott anyagcsere spektrum szerint hierarcikus sorozatba, rendezhetők. E sorozatnak léteznek szélsőértékei, amelyek valószínűsíthetően az elemi rendszerek, és a galaxisok környékén keresendők.
A galaxisok egész csillagrendszereket bontanak és a bontott csillaganyagot az elemi rendszerekhez közeli rendszerszinteken relatív nagy távolságokra, a fénysebességnél nagyobb külső mozgástartalommal szétsugározzák. Nem csak a galaxisok bontócentruma működik így, így működik az összes létező rendszer bontócentruma. A bontócentrumok fraktál alakzata hasonlóan működik, mint egyfajta fraktál konstrukciójú térszivattyú, amely a rendszerek környezetében lévő parciális tereket magába szippantva kifordítja a teret. Ez a hasonlat talán eredetmonda szintűnek tűnik de jó eséllyel illeszkedik a létező valósághoz.
Most térjünk vissza a "galaktikus vendéglő és kávézás" lehetőségére. A hagyományos szemléleten alapuló tanulással fejlesztett elme, a valós háromdimenziós térelképzelést fogadja el minden víziója ehhez illeszkedik, ebben a térben nem léteznek források és nyelők. Az új természetszemlélet szerint a rendszerek egymásba csomagolt, mozgások által kifeszített virtuális fraktál terekben léteznek, de a valós háromdimenziós térben jelennek meg a mi számunkra. A rendszerterek forrásokkal és nyelőkkel rendelkeznek, e források és nyelők azonos térpontokhoz, konkrétan a bontócentrumokhoz kapcsolhatók. A bontócentrumokon keresztül haladó rendszerminőségek elemeikre, alrendszereikre bomlanak, ezért nem kerülhetnek más idő-, és térkörnyezetbe. Az előzők alapján célszerűnek látszik az ebédutáni kávét a szokott helyen elfogyasztani.
¤¤ Az idő és a tér természete: Az idő és a tér fogalmi meghatározásával, tartalmi lényegének megragadásával sokan próbálkoztak, a próbálkozások színesek, de nem illeszkednek a létező valóság jelenségeihez. A létező valóság túl van a hagyományos gondolkozásmód hatókörén, és minden elképzelést meghaladó módon összetett.
Az új természetszemlélet megközelítése szerint az idő és a tér is rendszerminőség, és rendszerekhez kapcsolt módon léteznek, ebből következően irányminőséggel rendelkeznek, vetületben észlelhetők, fraktál természetűek, a kölcsönhatásokban keletkeznek és megszűnnek. A sor tovább is folytatható, ugyanis ha rendszerminőségek, akkor az öszes rendszerminőségekkel kapcsolatos felismerés esetükben is alkalmazható. A virtuális térben létező rendszerminőségek parciális viselkedést tanúsítanak, e viselkedés részeként autonóm parciális teret és időléptéket jelenítenek meg. Minden rendszer és minden alrendszer léte saját időszámítással kezdődik. Nem létezik abszolút idő és abszolút tér, ha egy rendszer megszűnik, akkor ezek a részminőségek is megszűnnek. A természet nem olyan mint egy asztali számítógép, amely automatikusan tárolja a korábbi beállításokat esetleges helyreállítás céljából, ezért nem mehetünk vissza az időben, nem tehetünk időutazásokat sem a múltba, sem pedig a jövőbe. Az univerzum minden jelensége egyszeri és megismételhetetlen.
¤ Anyag és antianyag: Az interneten kutatva az úgynevezett "antianyag" mibenléte és fogalmi meghatározása után, színes elképzelésekkel találkozhat a közönséges halandó. Az egyik forrás így vélekedik: Miért van több anyag, mint antianyag az Univerzumban? Honnan származik ez az aszimmetria? A modern kozmológia egyik legrégebbi, máig megoldatlan kérdése ez." Az egyik mértékadó forrás szerint: "Az antianyagban az atomot a proton, a neutron, és az elektron helyett azok antirészecskéi építik fel" Na ez megnyugtatónak tűnik, de mik azok az antirészecskék? Egy másik forrás szerint: "Az antirészecskék az elemi részecskék "tükörképei", tömegük és spinjük egyező, töltésük, mágneses momentumuk és más kvantum jellemzőik előjele azonban ellentétes."
Mit üzen az új természetszemlélet e különös jelenséggel kapcsolatban? Első lépésként talán az "anti anyag" fogalom tartalmi lényegét kellene tisztázni. Az új természetszemlélet nem használja az anyag fogalmat, helyette a rendszer és a rendszerminőség fogalmakat használja amelyek tartalmi értékkészlete nem szűkül le az atomok és alkotórészeik szintjére. Az antianyag fogalmával szemben tehát az anti rendszerek és rendszerminőségek létezését kellene megvizsgálnunk, amiket egyfajta tükörkép alakban kellene keresnünk, de tisztában vagyunk vele, hogy nem egyszerű molekula alakzatok tűkörképéről, hanem belső tartalmi tükörképről van szó.
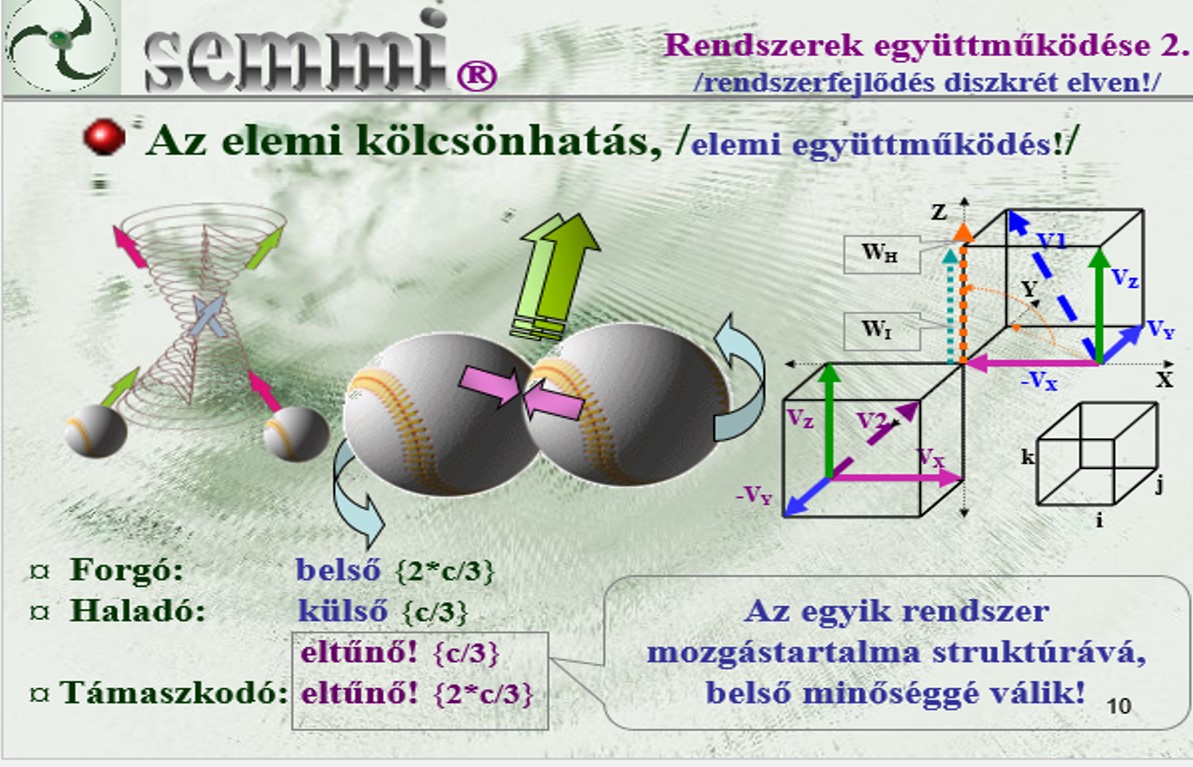 A
kérdés megközelítése érdekében vizsgáljuk meg az elemi kölcsönhatások
jelenségét, az egymáson legördülő golyók, vagy labdák hasonlatából
eszkábált modell segítségével. A dolgozat egyik elképzelése szerint, ha
két hasonló méretű golyó találkozik egymással, és a külső
mozgástartalmuk vektorai illeszkednek egy, egyköpenyű forgási
hiperboloid ellentétes oldali alkotóihoz, akkor egy ideig együtt
haladva közös minőséget jelenítenek meg. E közös minőség az új
rendszerminőség. Az új rendszerminőség külső és belső mozgástartalma a
találkozó golyók külső mozgástartalmából alakul ki. Az új
rendszerminőség külső mozgástartalma a találkozó alrendszerek egymással
párhuzamos mozgáskomponenseivel azonos, a belső mozgástartalmak pedig a
külpontos találkozásból eredő perdületből, vagy rotációból, valamint az
egymás felé mutató egymásra támaszkodó jellegű eltűnő
mozgáskomponensből tevődik össze. A kölcsönhatás tartalma vektorszorzat
jellegű.
A
kérdés megközelítése érdekében vizsgáljuk meg az elemi kölcsönhatások
jelenségét, az egymáson legördülő golyók, vagy labdák hasonlatából
eszkábált modell segítségével. A dolgozat egyik elképzelése szerint, ha
két hasonló méretű golyó találkozik egymással, és a külső
mozgástartalmuk vektorai illeszkednek egy, egyköpenyű forgási
hiperboloid ellentétes oldali alkotóihoz, akkor egy ideig együtt
haladva közös minőséget jelenítenek meg. E közös minőség az új
rendszerminőség. Az új rendszerminőség külső és belső mozgástartalma a
találkozó golyók külső mozgástartalmából alakul ki. Az új
rendszerminőség külső mozgástartalma a találkozó alrendszerek egymással
párhuzamos mozgáskomponenseivel azonos, a belső mozgástartalmak pedig a
külpontos találkozásból eredő perdületből, vagy rotációból, valamint az
egymás felé mutató egymásra támaszkodó jellegű eltűnő
mozgáskomponensből tevődik össze. A kölcsönhatás tartalma vektorszorzat
jellegű. Most szemléljük a modellt a józan észre hagyatkozva, ha a két golyó egymáshoz simuló és egyező irányú pályákon halad, akkor az azonos irányú mozgáskomponensek relatív nagyok, azaz relatív hosszú ideig képesek egymás környezetében lenni és közös minőséget megjeleníteni. Ellentétes irányú mozgástartalmak esetén a golyók relatív rövid idő alatt elhagyják egymás környezetét, még mielőtt közös minőséget tudnának megjeleníteni. Az ilyen találkozások bontó jellegű kölcsönhatásokként értelmezhetők.
Most szemléljük a jelenséget a mozgásvektorok aspektusából. Egyező irányú külső mozgásvektorok jobbsodrású, amígy az ellentétes irányú mozgásvektorok balsodrású rendszereket alkotnak. Amíg a jobbsodrású rendszerek esetében a vektorszorzat jellegű kapcsolatokban a külső mozgástartalom vektor, és a belső rotáció vektor azonos irányításúak, addig a balsodrású rendszerek esetében ezek a vektorok ellentétes irányúak. E megfontolások képezik alapját a következő kijelentésnek: "Tartós elemi együttműködés esetén a külső és a belső mozgástartalmak egyező irányítottságúak. Ez a feltétel a jobbsodrású rendszert alkotó struktúra és állapotelemek együttműködésénél teljesül."
Az azonos abszolút értékű, de ellentétes irányminőségű, jobb-, és a balsodrású vektorkapcsolatok egymás tükörképei, ezért tartalmi illeszkedést mutatnak az anyag-antianyag ellentétes minőségekkel. E gondolatsor alapján kijelenthető antianyag jellegű minőségmegjelenítés csak zérus közeli időléptékek esetén lehetséges, de magasabb rendszerszinteken ennek esélye szinte zérus. Általánosítva kijelenthető az elemi részek és az ő általuk alkotott úgynevezett primer tér aszimmetriájából következően a balsodrású rendszeregyüttműködések, vagy köznapi szóhasználattal élve az úgynevezett "antianyag" léte szinte kizárt. /E kérdésekkel részletesebben a negyedik dolgozatrész foglalkozik/
A dolgozat nyolcadik része foglalkozik hasonló kérdésekkel, egyértelmű, de meghökkentően különös válaszok jelennek meg a Fraktál Univerzum élő rendszerminőségivel kapcsolatban.
Az új természetszemlélet szerint: "A létező valóság fraktál természetű és egyetlen fraktál konstrukciót alkot." A természet fraktál minden eleme önmaga is fraktál. E különös jelenség, a diszkrét, csoportos, és kombinált kölcsönhatások ismétlődő sorozatai által jön létre. A kölcsönhatások valamennyien visszavezethetők az elemi kölcsönhatásra amelynek tartalmi lényegét az úgynevezett téraktivitás függvény fejezi ki:
{A(g) = k(sin(g) - cos(g)) = f(g) +f '(g)}.
A természet fraktál modellezhető az úgynevezett kölcsönhatás fraktál alakzat segítségével is, e fraktál minden eleme, egymásba ágyazott téraktivitás függvényekként azonosítható. Más aspektusból szemlélve a természet fraktál minden eleme függvény és differenciálhányadosa elemekként létezik, ők lineáris értelemben függetlenek egymástól és megfeleltethetők a struktúra, valamint az állapot alrendszer minőségeknek.
A téraktivitás függvénynek léteznek úgynevezett hierarchikus és parciális jellegű megoldásai, ők mind a természet fraktálon belül önálló alakzatokat képviselnek és egymásra közel merőleges irányminőségüek. A hierarchikus és a parciális fraktál alakzatok szélsőértékek és léteznek átmeneti alakzataik is, ők a szélsőértékek lineáris kombinációiként azonosíthatók.
Most tegyünk egy gondolati kitérőt és szemléljük Gánti Tibor "Chemoton" elméletét. A chemoton egy modell, amely a kémiai elemek által létrehozható önálló müködést tanúsító automatát jelöl, más kifejezéssel élve a chemoton egy kémiai masinéria. E különös szerzetek sokan léteznek és fejlődési sorozatba rendezhetők. E fejlődési sorozat felső szélsőértékei, határátmenetben úgy viselkednek mint az élő szervezetek alsó szélsőértékei, építőelemei.
A dolgozat elképzelései szerint a chemoton modell, a kémiai automaták, vagy a kémiai masinériák gondolata, a fraktál önhasonlóság elvét alkalmazva, kiterjeszthető minden rendszerszintre. Ebben az esetben nem kémiai masinériákról, hanem rendszerautomatákról kell beszélnünk. A rendszerautomaták jelensége logikailag illeszkedik az új természetszemlélethez, és a természet fraktál parciális ágaként azonosíthatók. Más fogalomhasználattal élve, a rendszerautomaták a természet fraktál parciális levelét alkotják. E fraktál konstrukción belül is elkülöníthető egy további szélsőérték. A rendszerautomaták e különös szélsőértékei azonosíthatók az úgynevezett élet fraktál jelenségként. Az új természetszemlélet egységes és ellentmondásmentes lokikai építménynek tűnik, és ebből az következik, hogy a természet fraktál ténylegesen rendelkezik olyan szélsőértékkel amely élet fraktálként azonosítható.
E megközelítésre alapozva kijelenthető: a természet fraktál eleme a rendszerautomata fraktál és ezen belül létezik az élet fraktál. Ha ez a kijelentés illeszkedik a létező valósághoz, akkor ebből további következtetések adódnak. Tekintsünk át néhány elemet a következtetések eseményhalmazából:
¤¤¤ Az univerzumban az élet minden rendszerszinten létezik,
és fraktál természetű
¤¤¤ Élőt élő hozhat létre, élő anyagcserekészletében élők szerepelnek
¤¤¤ Az élet nem kapcsolható egyetlen térkörnyezethez
¤¤¤ Az élők és nem élők között léteznek átmeneti jelenségek
¤¤¤ Az élők osztály szinten hasonlók
¤¤¤ Az élet fraktál, folyamatosan átrendeződő időtlen jelenség
Most szemléljük e kijelentések konkrét esetekre lokalizált jelentéstartalmát:
¤¤¤ Ha az élet, fraktál természetű, és minden rendszerzinten létezik, akkor a biológiai és az atomi rendszerszintek alatt és e felett is létezik. A különféle rendszerszinteken létező életjelenségek osztály szinten hasonlók, de természetszerűen nem humanoid jellegűek, és számunkra nem okvetlenül észlelhetők. E kijelentésekből adódóan léteznie kell a bolygó szint feletti életjelenségeknek is, amelyekhez intelligencia is társítható. Kijelenthető létezik szuperintelligencia, de nem mindenhatóról van szó, aki azonosítani képes bennünket és tetteinket egyedenként, viszont anyagcsere folyamatainkra képes meghatározó módon befolyással lenni. A felettünk lévő szuperintelligencia valószínűsíthetően hasonlóan viszonyul hozzánk, mint ahogy mi viszonyulunk az emésztő rendszerünkben létező baktérium tenyészetekhez.
¤¤¤ Ha az élet, fraktál természetű és e fraktál szélsőérték jellegű, akkor ezt a fraktál konstrukciót szélsőérték jellegű algoritmus képes létrehozni. Ez az algoritmus a téraktivitás függvények szélsőértéket képviselő megoldásaiként értelmezhetők, a már említett parciális együttműködésekként. Ebből az következik, hogy az életjelenségek fraktál alakzatát az élők együttműködése vagy részbeni együttműködése hozhatja létre. Profán, kisarkított, értelmező példával élve, nem lehet kis krokodilt kockacukorból szintetizálni, mert ő az atomi, és az atommag szintje alatti rendszerszinteken is kis krokodilból van.
¤¤¤ Ha az élet a természet fraktál rész alakzata, akkor nem köthető az univerzum kitüntetett térpozícióihoz, azaz mindenhol létezik. Az élők osztály szinten hasonlók, de változó jelenségek, ezért más élőhelyeken, vagy más redszerszinteken az általunk elképzelhetőtől teljes mértékben különböző formák is létezhetnek. /Gyakorlati példaként gondolhatunk közeli rokonainkra az egerekre ,ők is emlősők, meg mi is.../ Az életformák időben is változó jelenségek. /Gondolhatunk a periodikus kipusztulási jelenségekre és az új életformák megjelenésére./
¤¤¤ Az életjelenségek, egyedenként kipusztíthatók, időléptékekhez köthető élettartamúak, de összességükben, az élet fraktál maga kipusztíthatatlan és időtlen jelenség.
8. "Képmentes képtárak" és a sors könyve
® Létezik a sors könyve, vagy ez csak vallásfilozófiai kategória? A dolgozat tizenegyedik "Képmentes képtárak" részében szereplő hipotézis szerint: "A múlt, a jelen és jövő minden lehetséges eseménye a bináris jelekbe zárva, a jelek által képviselve, időtlen módon létezik!". A különös kijelentés tartalmának megértését segítheti, ha a szám fraktál bináris jel alakzatára gondolunk. A szám fraktál a rendszerminőségek összes lehetséges. abszolút-, és relatív viszonyának eseményhalmazát tartalmazza. A létező valóság az eseményhalmaz egyes elemeit jelníti meg, nem ismétlődő kombinációkban, a "Nagy Egész" folyamatos átrendeződései során. A szám fraktál abszolút módon létező, időtlen jelenség így bizonyos értelemben tekinthetjük a sors könyvének, de ez a könyv számunkra nem olvasható, nem elsősorban azért, mert a következő kombinációk nem jósolhatók meg, hanem azért mert az eseményhalmaz méretterjedelme számunkra kezelhetetlen. A sors könyve tehát elvileg létezik, de számunkra, gyakorlatilag nem létezik.
®® Léteznek képmentes képtárak, vagy ez csak valami polgárpukkasztó kijelentés? A "Képmentes képtárak" alcímet viselő dolgozatrész szerint léteznek. Miről van szó? Arról van szó, hogy a természet jelenségei leképezhetők, festmények, zeneművek, különféle dokumentumok és adathalmazok formájában, ezek az adathordozók elhelyezhetők például képtárakban, vagy más adattárakban ez az ismert gyakorlat, de ezzel szemben a dolgozat azt állítja, hogy a relatív nagyterjedelmű adathalmazok helyett elhelyezhetők bizonyos, relatív kisterjedelmű utasítások, amelyek segítségével az algoritmusok képesek előállítani a megfelelő adathalmazokat. A különös lehetőséghalmaz mellett új szemlélet bontakozik ki a dolgozat ösvényén barangolva. Közelítsük meg az új szemlélet tartalmi lényegét.
®®/1. A természet jelenségeinek eseményhalmaza illeszkedik a számfraktál jelenségéhez, így például kifejezhetők a szám fraktál bináris aspektusának alakjában is. Mielőtt tovább haladnánk, szembesülnünk kell a leképezés tényleges tartalmával, a dolgozat vonatkozó két hipotézise:
1. "A természetábrázolások közelítések, a természet bijektív módon nem leképezhető, a természet csak önmagával azonos."
2. "A természet digitalizált lenyomataiban az alrendszer minőségek viszonya helyett a választott bináris jelek viszonya jelenik meg."
®®/2.A második hipotézis szerint a jelenségek úgynevezett digitalizált változataiban a tartalmat, a választott bináris jelek viszonya hordozza. A bináris jelek választása, a jelterjedelmhez igazodó hibaintervallum választását is jelenti, más aspektusból szemlélve a jelenség bináris jelekkel történő leképezése csak egy bizonyos hibaintervallumon belül valósulhat meg. Most fókuszáljuk figyelmünket a kijelentés egyik részletére: ..a jelenségek részleteit az alrendszerek viszonya hordozza, a leképezés során e viszonyokat a bináris jelek külső viszonya hordozza. A dolgozat elképzelése szerint, az adathalmazokban szereplő diszkrét bináris jelekből képezhető egyetlen egy szuper bináris jel, e szuperjel belső viszonyaiban hordozza a leképezés tartalmát. A részletek mellőzésével megállapítható: a létező valóságot leképező bináris jelhalmazok, kölönféle csoportokba rendezhetők, e csoportok valamennyien a közös tartalmat képviselik. A közös tartalmú eseményhalmazban a tartalmakat a jelek külső és belső viszonyai hordozzák, az eseményhalmaznak szélsőértékei vannak, az egyik szélsőértékben a jelek külső-, a másik szélsőértékben a jelek belső viszonyai, az átmenetekben pedig a szélsőértékek kombinációi hordozzák a tartalmakat.
®®/3. Most fókuszáljuk figyelmünket a szuperjelre. A szuperjel, a leképezés diszkrét bináris jeleiből képzett egyetlen bináris jel, amely belső viszonyaiban hordozza a jelenség tartalmát. Minden szuperjel, bináris jel, így illeszkedik a szám fraktál bináris alakjához. A szám fraktál bináris alakját, annak bármelyik diszkrét-, vagy csoport elemét egyazon algoritmus képes előállítani, ami egyben azt is jelenti, hogy bármelyik természetleképezés, bármelyik szuperjelét ez az algoritmus képes előállítani. Ha egy konkrét természetleképezés szuperjelét szeretnénk előállítani, akkor meg kell mondani az algoritmusnak, hogy mikor, vagy melyik ponton hagyja abba a ciklikusan ismétlődő működést. Ennyi az egész, azonban ha ezt az utasítást a hagyományos észjárás szerint kívánjuk megadni, akkor a szuperjellel azonos bitterjeelmű utasításra van szükség, ennek tehát gyakorlati szempontból semmi értelme. A dolgozat felismerte milyen módon lehet relíatív kis jelterjedelmű utasításokkal vezérelni az algoritmust. Az algoritmus vezérelhető az úgynevezett fraktál függvények paraméterfüggvényei segítségével, a paraméterfüggvények konkrét értékeinek jelterjedelme relatív kicsi. E relatív kis jelterjedelmű utasítások segítségével az algoritmus képes előállítani az adott leképezéshez tartozó szuperjelet majd e szuperjelből a bináris jelhalmaz előállítható. Érzékelhető a képmentes képtárak nem tartalmazzák a képek digitalizált megfelelőit, ezek a képtárak csak a bináris jelhalmazokat előállító relatív kis jelterjedelmű algoritmus-vezérlő utasításokat tartalmazzák.
®®/4. Az új szemlélet lényegét a fraktál függvények megjelenése képviseli. A fraktál függvényeket algoritmusok hozzák létre, e függvények a hagyományos algebrai jelölésmódokkal nem adhatók meg, de számítógépek segítségével megjeleníthetők. /A fraktál függvények változói is függvények, nevezzük őket paraméterfüggvényeknek. A fraktál függvényekkel kiegészített függvényfogalom eseményhalmaza szélsőértékekkel rendelkezik. Az egyik szélsőértéket a jelenleg ismert függvények képviselik, amelyeknek egyetlen paramétere sem függvény, a másik szélsőértéket azok a fraktál függvények képviselik, amelyek minden paramétere függvény és minden paraméterfüggvénye szintén függvény./ A fraktál függvényeket és a szám fraktál elemeit azonos algoritmusok hozzák létre. Az algoritmus müködése különböző dimenziótartományokban követhető és megjeleníthető, ezen a módon a különböző dimenziótartományok között integrál tételek fogalmazhatók meg. Példaként tekintsünk háromparaméteres fraktál függvények esetére. A háromparaméteres fraktál függvények által képviselt felületek és térfogati integrál értékek tartalma illeszkedik az ismert Pascal háromszögek-, és az úgynevezett módosult Pascal háromszögek által képviselt felületekhez, valamint térfogatokhoz. Más aspektusból szemlélve egy-, kettő- és háromdiomenziós mérőszámok értékazonosságáról van szó. A jelenségek közötti illeszkedések újabb jelenleg még ismeretlen tartalmú kijelentéseket alapoznak meg. Vegyük példaként az adattárolás gyakorlatát, amely jelenleg ralatív nagy tárigénnyel és relatív kis gépmunkaidő ráfordítással történik. A fraktál függvények lehetőséget nyújtanak a relatív kis tárigényű és relatív nagy gépmunkaidő ráfordítású adattárolási eljárásokra, valamint a szélsőértékek közötti átmenetekre is. A jelenlegi gyakorlat előtt még ismeretlen ez a lehetőség, sajnálatos módon a gyakorlati alkalmazást nehezíti a gépmunkaidő ráfordítás hatványfüggvény szerinti változása. A gépmunkaidő különféle megoldásokkal szinte a kívánt mértékben csökkenthető, ennek ellenére a jövőben valószínűsíthetően a szupergyors számítógépeken történő alkalmazásokra számíthatunk.
9. Léteznek, jelenleg nem ismert matematikai
műveletek?
Az ismert matematikai
műveletek hierarchikus sorozatba rendezhetők, kérdés léteznek-e a sorozatnak
további elemei? A válasz igen, de nem egyszerű sorozatról-, hanem fraktál
viselkedésű jelenségről van szó, tehát a matematikai műveletek
megszámlálhatatlan elemterjedelmű halmazt alkotnak. Ez a kijelentés kissé
hihetetlennek, és polgárpukkasztó jellegűnek tűnik. E szerint a matematikai
műveletek egyfajta sajátos műveleti fraktál alakzatba rendezhetők. E műveleti
fraktál szélsőérték jellegű részhalmazaként értelmezhetők a jelenleg ismert
matematikai műveletek. A kijelentés tartalmának megértéséhez sajátos gondolati
ösvényen kell közelítenünk a jelenséget, ezt teszi a SEMMI 12. rész:” Az
analízis műveleti aspektusa” fejezetrész.
- o A számértékek
összerakhatók egység-, és nem egységelemekből az összeadás műveletével
- o A számértékek
összerakhatók a „szorzótényezők” segítségével, a szorzás műveletével.
- o A számértékek
összerakhatók a hatványozás műveletével.
- o A számértékek
összerakhatók integrál műveletekkel
- o A számértékek
összerakhatók az összeadás-, a szorzás-, a hatványozás-, és az integrál
műveletek, valamint az ellentétes irányú műveletek kombinációi segítségével is.
A felsorolás sorrendje egyben egyfajta hierarchiát is
rögzít, hiszen a hatványozás visszavezethető a szorzás-, a szorzás pedig az
összeadás műveletére, az integrálműveletek is összeadás jellegűek. Az eljárási
hierarchia, tartalmát tekintve függ a súlykészlet előállítási hierarchiájától,
de műveleti szempontból egy sorozatba rendezhető: összeadás, szorzás,
hatványozás, integrálás. Kérdés léteznek-e a sorozatnak további elemei?
Léteznek-e ismeretlen matematikai műveletek? A kérdés nem öncélú, polgárpukkasztó
jellegű, ez a kérdés az ismeretlen felé vezető ösvény irányát sejteti. Léteznek
tanult elmék, akik képesek kiegészíteni az előző okfejtést, hiszen a műveletek
különféle táblázatok, sorozatok, tömbök, mátrixok, tenzorok és függvények
esetére is értelmezhetők, továbbá a komplex mezőkre is lokalizálhatók, de
valamennyien úgynevezett skaláris jellegűek. Különös sajátossága e
műveleteknek, hogy valamennyien az összeadás elemi műveletére visszavezethetők.
A matematikai műveletek hierarchiája mellett érzékelhető a műveletek diszkrét
és a csoport jellege közötti hierarchia is. Értelmező példaként szemléljük az
elemi összeadás, a sorok összeadása, a táblázatok összeadása, vagy az integrál
műveletek összegzése műveletek közötti viszonyt.
Léteznek nem skaláris, azaz irányminőséggel rendelkező mennyiségek, és léteznek
az ő viszonyukban értelmezett műveletek is. Igen valóban, a vektorok közötti
összeadás műveletének eredménye a vektorok síkjában megjelenő összegvektor, a
vektorszorzás eredménye a vektorok síkjára merőleges irányú, tehát új dimenziót
képviselő eredményvektor, de milyen módon értelmezett a vektorműveletek
hierarchiája? Vektorok összeadása és szorzása definiált, de milyen módon
értelmezett a hatványozás művelete? A kérdés megközelítése érdekében szemléljük
az egységvektorok hatványozásának esetét, legyen a példaeset {(i ´ j)n}. A művelet kétféle módon is értelmezhető
aszerint, hogy a hatványozást a matematika jelenlegi gyakorlata szerint
skaláris műveletként-, vagy vektorműveletként értelmezzük. Az eredmény az első
esetben {(i ´ j)n = (k) n}
skaláris szorzat, a második esetben {(i ´ j)n
= (i ´ j) ´ (i ´ j) ´…. ´ (i ´ j) = k´k´….´k = 0}
vektorszorzat. Érzékelhető a vektorszorzat elvén működő úgynevezett „vektor-hatványozás”
nem működőképes művelet, ugyanis az értelmezés szerint a párhuzamos vektorok
szorzata zérusértékű.
A skaláris-, és vektorműveletek viszonya is hierarchikus jellegű, ugyanis a
vektorok viszonya skaláris komponensekkel jellemezhető, vagy más aspektusból
közelítve a kétdimenziós jelenségek rendelkeznek egydimenziós vetületi
minőségekkel, ezért a skaláris tér szemlélhető a vektortér vetületi
minőségeként. Más aspektusból közelítve a jelenséget a vektorműveletek
visszavezethetők skaláris műveletekre. Na remek megjelent az alapműveletek-, a
diszkrét és csoportműveletek-, valamint a skaláris és vektorműveletek
hierarchikus viszonya, most ismét tegyük fel a kérdést: léteznek-e a sorozatnak
további elemei?
Az egymástól lineáris értelemben független mozgáskomponensek által kifeszített
virtuális fraktál terekben sok egymástól lineáris értelemben független dimenzió
és térirány létezik. E térirányok nem közös koordináta kezdőpontokból, hanem a
szám fraktál zérus pontjaihoz illeszkedő, háromdimenziós, speciális görbült
koordináta rendszerek, kezdőpontjaiból indulnak. E terek fraktál terek és a
dolgozat elképzelése szerint, fraktál minőséget algoritmusok ismétlődő működése
képes létrehozni. Az algoritmus, tartalma szerint műveleti utasítás, a
matematikai műveletekhez is tartoznak műveleti utasítások, tehát ők is
azonosíthatók algoritmusokként. Ezek szerint:
Ha ez így van, akkor az algoritmusok halmazát kellene
a hierarchikus viszonyok aspektusából áttekinteni, ugyanis ez a viszony
azonosítható a matematikai műveletek viszonyaként is. Na remek milyen irányból
kezdhető a közelítés? Természetesen a rendszerszemléletű közelítés lehet
eredményes, amely szerint minden létező minőség rendszerminőség és minden
rendszerminőség fraktál természetű. Erről az alapról indulva kijelenthető a
létező algoritmusok, úgynevezett algoritmus fraktál alakba rendezhetők. Az
algoritmus fraktál rendszerszintekkel rendelkezik, a rendszerszintek, saját
léptékkel rendelkeznek és egyben dimenziószinteket is, képviselnek. A rendszerszintek
közötti viszony egész dimenziókülönbségekkel, a rendszerszintek elemei közötti
viszony tört dimenzió eltérésekkel jellemezhetők. Érzékelhető összetett
jelenséggel állunk szemben, hiszen amíg a dimenziószintek lineáris értelemben
független-, addig a dimenziószintek elemei lineáris kombinációik viszonyában
léteznek. E kijelentés megfogalmazható az elemek hierarchiája aspektusából is e
szerint:
/Az algoritmusok részletes vizsgálatára a dolgozat
harmadik részében kerül sor, de egyfajta rendszerezés található a „SEMMI –
Rendszerelmélet és Fraktál Univerzum” kiadványban is./
Most gondolatban térjünk vissza ismét az analízis jelenségéhez. A szó-alakhoz a
részekre bontás tartalmat rendeltük. A részekre bontás műveletei visszavezethetők
a matematika gyakorlatában értelmezett műveletekre. A matematika gyakorlatában
értelmezett műveletek algoritmusokként értelmezhetők, ezért ők részét képezik
az algoritmusok eseményhalmazának. Az algoritmusok eseményhalmaza fraktál
konstrukciót alkot, ezért a fraktál konstrukciókra vonatkozó rendszerelméleti
közelítések esetükben is alkalmazható. He ez a logikai okfejtés illeszkedik a
létező valósághoz, akkor a matematika gyakorlatában definiált műveletek
egyfajta hierarchikus sorozatának léteznek további sorozatelemei, amelyek
fraktál algoritmusokként azonosíthatók. Más aspektusból közelítve:
A fraktál algoritmusok fraktál konstrukcióba
rendezhetők, eseményhalmazuk nem megszámlálható, de bizonyos szempontok szerint
csoportosíthatók, azaz esetükben is alkalmazhatók az analízis módszerei. A
teljesség igénye nélkül tekintsünk át néhány csoportosítási lehetőséget:
o Léteznek
fraktál képző és fraktál lebontó algoritmusok.
o Fraktál
algoritmusok működhetnek önállóan és csoportos viszonyban, a csoportos működés
lehet soros, párhuzamos kölcsönható és kombinált jellegű.
o Fraktál
algoritmus, és algoritmus csoport az ismétlődő működés során lehet állandó-, és
változó tartalmú.
o Fraktál algoritmus,
a működés ismétlődéseitől, a ciklusszámtól függően létrehozhat skaláris-,
átmeneti-, és fraktál minőségeket.
o Fraktál
algoritmusok rangsorolhatók a dimenzió transzformáló képességeik szerint is.
o Fraktál
algoritmusok egymásba épülhetnek, az egymásba épülés lehet egyszerű csoport-,
vagy összetett, fraktál elvű.

Malárics Viktor , +36 30 210 1590, malaricsv45@gmail.com
¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤
Kezdő lap Dolgozatrészek Kérdések és válaszok